Optimization on Manifolds and Statistical Learning
In this article, I present a solution to Qube’s challenge that uses manifold optimization, a technique that I was unfamiliar with at the time of attempting the challenge. Since I found it to be an interesting and valuable approach, I decided to share what I learned through this blog post.
The Challenge
Introduction
The problem at hand involves estimating temporal vectors $R_t \in \mathbb{R}^n$ (representing stocks) using the following vectors: $$ S_{t+1} = \sum_l^L \beta_l F_{t, l} $$ where $F_{t, l} \in \mathbb{R}^{n}$ are referred to as “factors” at time $t$, there are $L$ of them, and $S_{t+1}$ is an estimator for $R_t$. This represents a linear regression between $R_t$ and $F_t$.
We want to estimate these factors using past vectors $R_{t-k}$ according to a specific structure: $$ F_{t,l} = \sum_k^D A_{k, l} R_{t+1-k} $$
where $A_l := (A_{k, l}) \in \mathbb{R}^D$ are vectors and $D$ is a fixed time depth parameter. We assume that the vectors $A_l$ are orthonormal, i.e. $\langle{l1}, A_{l2\rangle = \delta_{k, l}$.
In this article, we will use a simple LMSE loss for multiple output regression: $$ L(\hat{Y}, Y) = Tr((\hat{Y} - Y)^T (\hat{Y} - Y)) $$
For the challenge, we can implement the loss function with the following code, where the parameters and data are inputted:
def qube_loss(A, beta, X, Y):
""" """
diff = beta.T @ A.T @ X - Y
return np.trace((diff.squeeze().T @ diff.squeeze()))
Solving the problem is equivalent to the following optimization problem:
$$ \argmin_{A^T A = I_F} L(\hat{Y}(A, \beta, X), Y) $$
Solving the Problem with Manifold Optimization
As noted in the challenge description, the orthonormality constraint in the optimization problem can be interpreted as a search on the Stiefel Manifold. To solve the problem, we adapt conventional gradient descent algorithms for manifolds. The procedure involves the following steps:
Init $x_0$.
While $x_k$ has not converged:
- Compute the gradient $grad_k$ of the loss on the manifold
- Multiply the gradient by a “good” constant $t_k$
- Retract $- t_k * grad_k$ in A on the manifold to update $x_{k+1}$ return $x_k$
But what exactly is a manifold, and how do we compute the gradient and retract on it? In this post, we will provide rigorous definitions of manifolds, and explain how to compute gradients and retractions on them. We will also illustrate these concepts with the example of the Stiefel manifold and provide Python code. Finally, we will show how to use the optimization algorithm to solve Qube’s challenge.
Understanding Smooth Manifolds
Before delving into the optimization problem, let us first understand what a smooth manifold is. In simple terms, a manifold can be thought of as a geometric object that is locally linear. For instance, the sphere in $\mathbb{R}^3$ can be mapped continuously into a vector space $\mathbb{R}^2$ around any point on the sphere. This enables us to define an Euclidean coordinate system around any point on the sphere. This property of being able to transform a piece of a geometrical object into something interpretable with usual coordinate systems is what defines a manifold.
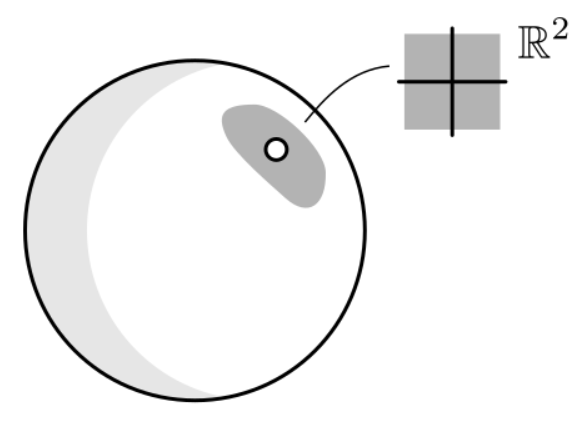
Charts Definition
We define a chart for $M$ as a bijective function $\phi$ of a subset $\mathcal{U}$ of $M$ onto an open subset of $\mathbb{R}^d$. Given this chart, for all $x \in \mathcal{U}$, $\phi(x)$ is called the coordinates of x in the chart $(\mathcal{U}, \phi)$.
Charts are how we translate each neighbors of the manifold into coordinates. If we have many charts for multiple neighborhoods, they need to be “coherent”, and this how we define atlases.
Atlases Definition
An atlas of a smooth manifold $M$ into $\mathbb{R}^d$ is a collection of charts $(\mathcal{U}{\alpha}, \phi{\alpha})$ such that the union of all $\mathcal{U}{\alpha}$ covers $M$ and the change of coordinates between any two charts is smooth. In other words, for any $\alpha, \beta$, the intersection $\mathcal{U}{\alpha} \cap \mathcal{U}{\beta}$ is nonempty and the maps $\phi{\beta} \circ \phi_{\alpha}^{-1}$ are smooth. We can think of an atlas as a set of compatible coordinate systems that cover the manifold. If two atlases are equivalent, meaning they have compatible charts, their union is also an atlas. The maximal atlas $A^+$ compatible with an atlas $A$ is called a differential structure on $M$.
Smooth Manifold
A $d$-dimensional manifold is a tuple $(M, \mathcal{A}^+)$, where $M$ is a set and $\mathcal{A}^+$ is a maximal atlas of $M$ into $\mathbb{R}^d$, such that the topology induced by $\mathcal{A}^+$ is Hausdorff and second-countable. The atlas $\mathcal{A}^+$ is referred to as a manifold structure. A chart $\phi$ gives rise to a local parametrization of $\mathcal{M}$ via $\phi^{-1}$. The requirement of Hausdorff and second-countable topologies is necessary to avoid pathological topological behavior.
Examples
Now that we have defined what a manifold is, let’s look at some examples to better understand the concept. According to the definition, if a set $M$ admits an atlas $\mathcal{A}^+$, it is likely a smooth manifold.
Set of matrices
First, let’s consider the set of matrices $\mathbb{R}^{n \times p}$. We can define a chart $\phi:\mathbb{R}^{n \times p}\rightarrow \mathbb{R}^{np}$ as follows: $\forall X \in \mathbb{R}^{n \times p}, \phi(X) = \text{vec}(X)$, where $\text{vec}$ is the stacking operation of all the column vectors of $X$. This chart allows us to define a manifold structure on the set of matrices.
Non Compact Stiefel Manifold
A more complex example is the non-compact Stiefel manifold, which is the set of matrices whose columns are linearly independent. This set is an open subset of $\mathbb{R}^{n \times p}$ and admits a chart using the same $\text{vec}$ function. Thus, $\mathbb{R}^{n \times p}_*$ (notation for the submanifold) has a manifold structure and is referred to as the non-compact Stiefel manifold.
Stifel Manifold
Finally, we call the Stiefel manifold the set of matrices whose columns are orthonormal, i.e $A^T A = I$ which corresponds to the constraint on our optimization problem. We can show that it is also admits a manifold structure. Let $V$ be an $n$-dimensional vector space, and consider the Stiefel manifold $V_{k} = {A \in \mathbb{R}^{n \times k} : A^TA = I_k}$, where $k \leq n$. For any $A \in V_k$, let $U_A = {B \in \mathbb{R}^{n \times k} : |B - A| \geq \epsilon}$ be a small open ball around $A$ (where $\epsilon$ is some small positive number), and define $\phi_A : U_A \to \mathbb{R}^{k(k-1)/2}$ by $$ \phi_A(B)=vec(B^TA−A^TB) $$
Note that $B^TA - A^TB$ is a skew-symmetric matrix (i.e., $C^T = -C$) that has $\binom{k}{2}$ independent entries. Thus, $\phi_A$ is a diffeomorphism onto its image, which is an open subset of $\mathbb{R}^{k(k-1)/2}$.
It can be shown that the collection of charts ${(U_A, \phi_A) : A \in V_k }$ forms an atlas for $V_k$, and that the transition maps between overlapping charts are smooth. Therefore, $V_k$ is a smooth manifold of dimension $k(n-k)$.
Consequently, since this is a manifold, we can do optimization on the manifold to solve the optimization problem.
Differentials and gradients on Manifolds
After introducing manifolds and the Stiefel manifold, let’s now focus on differentiability on a manifold for a given mapping.
Differentiability
Consider a mapping $F$ between two manifolds. A coordinate representation of $F$ for two charts $\phi_1$ and $\phi_2$ of the manifolds is defined as $\hat{F} = \phi_2 \circ F \circ \phi_1^{-1}$. We say that $F$ is differentiable or smooth at $x$ if $\hat{F}$ is $C^{\infty}$ at $\phi_1(x)$. This property does not depend on the choice of charts, based on the definition of atlases.
Tangent vectors
To define derivatives for real-valued functions on a manifold and compute gradients for optimization algorithms, we need to first define tangent vectors at a point on the manifold.
A tangent vector $\xi$ to a manifold $M$ at a point $x$ is a mapping from $\mathcal{F}_x$, the set of real-valued functions defined on a neighborhood of $x$, to $\mathbb{R}$. There exists a smooth curve $\gamma$ on $M$ with $\gamma(0) = x$ such that:
$$ \forall f \in \mathcal{F}_x, \xi_x(f) = \frac{d(f(\gamma(t)))}{dt}\Bigr|{\substack{t=0}} $$
This means that we define a tangent vector as the derivative of a certain real-valued function on the manifold composed with a smooth curve $f\circ \gamma$. The tangent space at $x$, denoted $T_x M$, is the set of all tangent vectors to $M$ at $x$. This set is a vector space, and we can prove that its dimension is $d$.
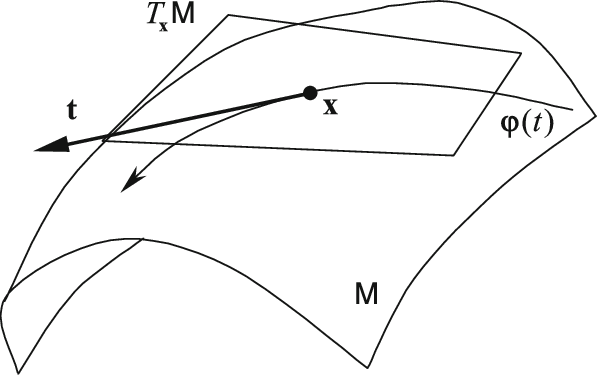
Differentials
Let $F: M \rightarrow N$ be a differentiable mapping between manifolds $M$ and $N$. The differential of $F$ at a point $x \in M$ is denoted by $DF(x)$ and defined as a linear transformation from the tangent space $T_x M$ at $x$ to the tangent space $T_{F(x)} N$ at $F(x)$, given by: $$ DF(x)[\xi_x]=\xi_x (f\circ F) $$
for any $\xi_x \in T_x M$ and any smooth function $f$ on $N$ defined on a neighborhood of $F(x)$.
Note that for real-valued functions, the differential can be easily defined using the identification $T_x\mathbb{R} \approx \mathbb{R}$, as follows: $$ DF(x)[\xi_x]=\xi_xF $$ where $F$ is a real-valued function on $M$.
Riemanian metric and Gradient
On a manifold, tangent vectors generalize the notion of a directional derivative, but we need a notion of length that applies to tangent vectors in order to characterize which direction of motion from a point x produces the steepest increase in a function f. To achieve this, we endow every tangent space T_xM with an inner product. Once we equip a manifold with a smoothly varying inner product, we obtain a Riemannian manifold.
With a Riemannian metric on a manifold, we can define a gradient as the direction of the steepest ascent of a function f at x. Specifically, for a tangent vector $\xi$ at $x$, the inner product between the gradient of $f$ at $x$ and $\xi$ is given by
$$ \langle grad f(x) | \xi \rangle_x = Df(x)[\xi] $$
To compute a gradient more easily, we can use the fact that manifolds embedded in another manifold, typically $\mathbb{R}^n$, inherit some of the properties of the function defined on the manifold. For example, if a manifold M is endowed with a Riemannian metric, then manifolds generated from M, such as submanifolds and quotient manifolds, can inherit a Riemannian metric in a natural way.
In the case of embedded submanifolds, the Riemannian metric g of the larger manifold M induces a Riemannian metric g on the submanifold M. To compute a gradient of a function defined on the submanifold, we can project the gradient of the function defined on the larger manifold onto the tangent space of the submanifold
Gradient of Qube’s loss on Stiefel manifold
Tangent space on Stiefel manifold
Let’s first compute the tangent space at any point $x$ of the manifold. To compute the tangent space at any point $x$ of the Stiefel manifold, we use the tangent space at the identity matrix $I_p$. This is because the Stiefel manifold is a homogeneous space and has a constant tangent space at all points. We can obtain the tangent space at any point $x$ by left multiplication with $x$, which acts as a diffeomorphism between the tangent space at $I_p$ and the tangent space at $x$.
The tangent space at $I_p$ consists of all matrices of size $p \times n$ with the property that they are skew-symmetric ($\xi^T = -\xi$) and satisfy $X^TX = I_p$. In other words, they are the matrices that are orthogonal to the columns of $X$ and have the same dimensions as $X$. The dimension of the tangent space is $p \times n - p(p+1)/2$, which is the same as the dimension of the manifold.
Projection on normal and tangent space of Stiefel manifold
The Riemannian metric inherited from the embedding space $\mathcal{Rn \times p}$ is $$ \langle\xi, \eta\rangle_X := tr(\xi^T \eta) $$
If $\xi = X\Omega_{\xi} + X_{\perp}K_{\xi}$ and $\eta = X\Omega_{\eta} + X_{\perp}K_{\eta}$ then $\langle\xi, \eta\rangle_X = tr(\Omega^T_{\xi}\Omega_{\xi} + \Omega_{\eta}^T\Omega_{\eta}$. In view of the identity $tr(S^T \Omega) = 0$ for all $S \in S_{sym}(p)$, $\Omega \in S_{skew}(p)$, the normal space is: $$ (T_X St(p, n))^{\perp} = {XS : S ∈ S_{sym}(p)}. $$ The projections are given by $$ \begin{aligned} P_X \xi = (I - XX^T)\xi + X skew(X^T \xi) \\ P_X^{\perp} \xi = X sym(X^T \xi) \\ \end{aligned} $$ where $sym(A) := \frac{1}{2}(A + A^T )$ and $skew(A) := \frac{1}{2} (A − A^T)$ denote the components of the decomposition of A into the sum of a symmetric term and a skew-symmetric term.
Computation of the gradient for Qube’s loss
Now, back to our definition, we are ready to compute the gradient of the loss on the manifold. We need:
1 the gradient of the loss $\bar{L}$ which is the continuation of the loss $L$ defined on $\mathbb{R}^{L + D}$:
def gradient_qube_loss_bar(A, beta, X, Y, mu_A, mu_beta):
""" """
grad_A = 2 * beta @ (beta.T @ A.T @ X - Y) @ t_part(X)
grad_beta = 2 * (beta.T @ A.T @ X - Y) @ t_part(X) @ A
return grad_A.sum(axis=0).T + mu_A * A, grad_beta.sum(axis=0).T + mu_beta * beta
The formula is obtained with usual algebric computations. Note that we added a regularization term for both $A$ and $beta$.
- The projection function on the tangent at a point $A$:
DIM_D = 250
def P_A(A, H):
"""
Project H to the tangent space at point A
"""
PX_H = (np.eye(DIM_D) - A @ A.T) @ H + 1 / 2 * A @ (A.T @ H - H.T @ A)
return PX_H
Now the gradient relative to the parameters $A$ is obtained by projecting the gradient of $\bar{L}$ on the tangent space of the manifold. The gradient for $\beta$ is not projected because there are no constraints on them.
def gradient_qube_loss(A, beta, X, Y, mu_A, mu_beta):
""" """
grad_A, grad_beta = gradient_qube_loss_bar(A, beta, X, Y, mu_A, mu_beta)
grad_A = P_A(A, grad_A)
return grad_A, grad_beta
Line-Search Algorithm on Manifolds
Retractions
A retraction on a manifold $M$ is a smooth mapping $R$ from the tangent bundle $T_M$ onto $M$. A retraction at point $x$, denoted by $R_x$, is a mapping from the tangent space $T_xM$ to $M$ with a local rigidity condition that preserves gradients at $x$. The retraction will be useful for gradient descent to map the descent from the tangent space at a point $x$ back to the manifold. A retraction $R$ at $x$ satisfies the following properties:
(i) $R_x(0_x) = x$, where $0_x$ denotes the zero element of $T_xM$.
(ii) With the canonical identification $T_{0_x} T_x M \cong T_xM$, $R_x$ satisfies $DR_x(0_x) = id_{T_xM}$, where $id_{T_xM}$ denotes the identity mapping on $T_xM$.
Retraction on the Stiefel manifold
For the Stiefel manifold, two alternative choices for a retraction are:
- $R_X(\xi) = (X + \xi)(I_p + \xi^T \xi) − \frac{1}{2}$, where we have used the fact that $\xi$, as an element of $T_X St(p, n)$, satisfies $X^T \xi + \xi^T X = 0$.
- $R_X(\xi) := qf(X + \xi)$, where $qf(A)$ denotes the $Q$ factor of the decomposition of $A \in \mathbb{R}^{n \times p}_*$ as $A = QR$, where $Q$ belongs to $St(p, n)$ and $R$ is an upper triangular matrix with strictly positive diagonal elements.
The following Python code implements those retractions :
DIM_L = 10
def retract(Z, A):
"""
Retraction of Z from the tangent space in A to the Stiefel manifold
"""
q, r = np.linalg.qr(Z + A)
return q
def retract_0(Z, A):
"""
Retraction of Z from the tangent space in A to the Stiefel manifold
"""
s = np.sqrt(np.eye(DIM_L) + Z.T @ Z)
A_next = (A + Z) @ inv(s)
return A_next
Gradient Descent algorithm
Line-search methods on manifolds are based on the update formula: $x_{k+1} = R_{x_k} (t_k\eta_k)$, where $\eta_k$ is in $T_{x_k}M$ and $t_k$ is a scalar. Once the retraction $R$ is chosen, the two remaining issues are to select the search direction $\eta_k$ and then the step length $t_k$. Typically, we choose the gradient as $\eta_k$, and $t_k$ is chosen using K-Fold search.
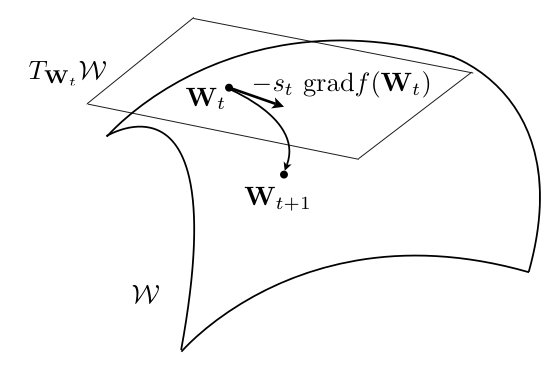
The following Python code implements the gradient descent algorithm using line search on the Stiefel manifold:
def opti_qube_loss(A_0, beta_0, X, Y, epsilon=1e-03, N=100, mu_A=1e-05, mu_beta=1e-05, t_k=0.06, gamma_k=0.06):
""" """
A_k, beta_k = A_0.copy(), beta_0.copy()
i = 0
while qube_loss(A_k, beta_k, X, Y) > epsilon and i < N:
A_k, beta_k = line_search_next(A_k, beta_k, X, Y, mu_A, mu_beta, t_k, gamma_k)
i += 1
print(i, qube_loss(A_k, beta_k, X, Y), metric_train(A_k, beta_k, X, Y))
return (A_k, beta_k)
def qube_loss(A, beta, X, Y):
""" """
diff = beta.T @ A.T @ X - Y
return np.trace((diff.squeeze().T @ diff.squeeze()))
Full Implementation and Results
The complete implementation is provided below as a Python code block. While the theoretical aspects of the algorithm may appear complicated, the implementation itself is actually quite simple and requires very few lines of code. Our initial results were quite promising, as we achieved a top 10 ranking during the first months, but we did not attempt to further optimize the algorithm. It is worth noting that there are many other optimization algorithms available and regularization techniques that could potentially enhance the performance of the model.
import numpy as np
from numpy.linalg import inv
from utils import *
def opti_qube_loss(A_0, beta_0, X, Y, epsilon=1e-03, N=100, mu_A=1e-05, mu_beta=1e-05, t_k=0.06, gamma_k=0.06):
""" """
A_k, beta_k = A_0.copy(), beta_0.copy()
i = 0
while qube_loss(A_k, beta_k, X, Y) > epsilon and i < N:
A_k, beta_k = line_search_next(A_k, beta_k, X, Y, mu_A, mu_beta, t_k, gamma_k)
i += 1
print(i, qube_loss(A_k, beta_k, X, Y), metric_train(A_k, beta_k, X, Y))
return (A_k, beta_k)
def qube_loss(A, beta, X, Y):
""" """
diff = beta.T @ A.T @ X - Y
return np.trace((diff.squeeze().T @ diff.squeeze()))
def line_search_next(A_k, beta_k, X, Y, mu_A, mu_beta, t_k, gamma_k):
""" """
grad_A, grad_beta = gradient_qube_loss(A_k, beta_k, X, Y, mu_A, mu_beta)
# TODO: Avoid Brute force
A_k = retract(-t_k * grad_A, A_k)
beta_k += -gamma_k * grad_beta
return A_k, beta_k
def gradient_qube_loss(A, beta, X, Y, mu_A, mu_beta):
""" """
grad_A, grad_beta = gradient_qube_loss_bar(A, beta, X, Y, mu_A, mu_beta)
grad_A = P_A(A, grad_A)
return grad_A, grad_beta
def gradient_qube_loss_bar(A, beta, X, Y, mu_A, mu_beta):
""" """
grad_A = 2 * beta @ (beta.T @ A.T @ X - Y) @ t_part(X)
grad_beta = 2 * (beta.T @ A.T @ X - Y) @ t_part(X) @ A
return grad_A.sum(axis=0).T + mu_A * A, grad_beta.sum(axis=0).T + mu_beta * beta
def P_A(A, H):
"""
Project H to the tangent space at point A
"""
PX_H = (np.eye(250) - A @ A.T) @ H + 1 / 2 * A @ (A.T @ H - H.T @ A)
return PX_H
def retract(Z, A):
"""
Retraction of Z from the tangent space in A to the Stiefel manifold
"""
q, r = np.linalg.qr(Z + A)
return q
def retract_0(Z, A):
"""
Retraction of Z from the tangent space in A to the Stiefel manifold
"""
s = np.sqrt(np.eye(10) + Z.T @ Z)
A_next = (A + Z) @ inv(s)
return A_next
Conclusion
In this article, we have explored the concept of optimization on manifolds, which is a powerful tool for solving optimization problems with complex structures. We have introduced the idea of the Stiefel manifold, which is a manifold of orthogonal matrices that arises naturally in various applications, such as signal processing, statistics, and machine learning.
A useful reference book for optimization on manifolds is “Optimization Algorithms on Matrix Manifolds” by Absil, Mahony, and Sepulchre, which provided me a comprehensive treatment of the subject and includes many practical examples and applications.