Functional programming and category theory are two related fields in mathematics and computer science that can be used to design and solve complex problems. Functional programming, as I explained in the previous articles, is a programming paradigm that emphasizes the application of functions, while category theory is an abstract mathematical system that can be used to analyze and compare objects and their relationships. By combining both of these fields, it is possible to create powerful and efficient applications. Category theory deals with the study of structure, relationships between objects, and morphisms (mappings or functions) between them. It provides a foundation for functional programming by allowing us to abstract common features and express relationships between objects and functions. Category theory also allows us to create new objects and operations by combining existing ones into larger structures. In programming, it is often used to describe abstract concepts such as data types, monads, and functors.

What is a category ?

A first definition

A category $C$ is composed of:

• Objects noted $ob(C)$
• Morphisms (or arrows) noted $hom(C)$. Each arrow has a domain, and a codomain which are both objects. Morphisms can be viewed as arrows from the domain to the codomain. Morphisms $f$ from an object $A$ to an object $B$ is denoted as $f: A \rightarrow B$.
• A binary operation $hom(a, b) × hom(b, c) → hom(a, c)$ called composition. The composition of $f : a \rightarrow b$ and $g : b \rightarrow c$ is written as $g \circ f$. Composition should be associative.
• For every object $x$, there exists a morphism $Id_x : x \rightarrow x$ called the identity morphism for $x$, such that every morphism $f : a \rightarrow x$ satisfies $Id_x \circ f = f$, and every morphism $g : x \rightarrow b$ satisfies $g \circ Id_x = g$.

In Category Theory, we are studying structures called categories which highlight objects and their relationships to other objects. Those relationships verify the composition property, which you should recognize as something familiar as it appeared naturally in classical mathematics. For example, in Set Theory, if you take a set A, a set B, and a set C and if there is a function $f: A \rightarrow B$ and a function $g: B \rightarrow C$, then there exists a function $h: A \rightarrow C$. This function is $h = g \circ f$. So sets could be a good candidate to define a category. This will be our first example, and this category is named $\mathbf{Set}$.

Example of the category of sets

$\mathbf{Set}$ is defined as the category where the objects are sets, and where the morphisms between sets A and B are the functions from A to B, and the composition of morphisms is the composition of functions.

This first example demonstrates that categories are simple structure, and that we already knew one of them. An important remark is that while Set Theory emphasize the importance of objects and their contents, Category Theory study the relationship between objects, and do not study what’s going on inside the object. In a way, the categoricist consider that by studying the relations between objects, we can deduce enough properties on the objects, but most importantly, on the structure itself.

Functional programming languages as categories

Interest in category theory among computer scientist is due to the fact that the constructions in FP make the language similar to a category. Let’s describe the similarities informally.

Functional Programming Languages

In functional programming languages, we write algorithms as functions, using primitive types and operations, and some constructors from which one can produce more complicated types and operations (cf. previous article). In this sense, computing a value is only the result of applying constructors to the types, constants and functions.

The language has:

• Primitive data types, such as boolean.
• Constant of each type, such as True for booleans
• Operations, which are functions between the types
• Constructors which can be applied to data types and operation to produce derived data types and operation of the language.

Category of types as a model for FP

To construct a category for any FP language, we add the following assumption:

1. There is a unit function $Id_A$ for each type $A$. When applied, it does nothing to the data
2. We add another primitive type named $1$, which is an terminal object. We interpret each constant $c$ of type $A$ as an arrow $c: 1 \rightarrow A$.
3. We assume that the language has a composition constructor $\circ$.

Under those conditions, a functional programming language has a category structure:

• The types are the object of the category
• The operations are the morphisms
• The source and target of an arrow are the input and output types
• Composition is given by the composition constructor
• The identity morphisms are defined.

Example

Let’s suppose we have a simple language with two data types, $\mathbf{NAT}$ and $\mathbf{CHAR}$. We have the following operations and constants:

• $\mathbf{NAT}$ should have a constant $0: 1 \rightarrow \mathbf{NAT}$ and an operation $succ: \mathbf{NAT} \rightarrow \mathbf{NAT}$.
• $\mathbf{CHAR}$ should have one constant $c: 1 \rightarrow \mathbf{CHAR}$ for each desired character $c$.
• There are two type conversion operations $ord: \mathbf{CHAR} \rightarrow \mathbf{NAT}$ and $chr: \mathbf{NAT} \rightarrow \mathbf{CHAR}$ such that $chr \circ ord = id_{\mathbf{CHAR}}$.

Thus, we can define a new operation $next$ which computes the next character in order:

$$next = chr \circ succ \circ ord : CHAR \rightarrow CHAR$$

Functors

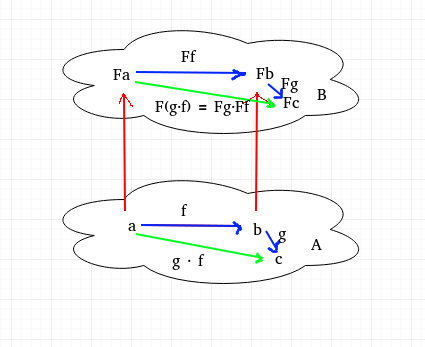
A functor can be thought as a morphism between categories. Functors are important for a programmer because they allow developers to abstract data and create a structure that can be used across different programs. By implementing a functor, developers can ensure that the same type of data is being processed in a consistent manner, and convert functions from types to other constructed type. Let’s first review the definition given by wikipedia:

Definition of a functor

Let $C$ and $D$ be categories. A functor $F$ from $C$ to $D$ is a mapping that

• associates each object $X$ in $C$ to an object $F(X)$ in $D$

• associates each morphism $f: \to Y$ in $C$ to a morphism $F(f): F(X) \to F(Y)$ in $D$ such that the following two conditions hold:

  • $F(Id_{X}) = Id_{F(X)}$ for every object $X$ in $C$

  • $F(g\circ f)=F(g)\circ F(f)$ for all morphisms $f\colon X\to Y$ and $g\colon Y\to Z$ in C.

That is, functors must preserve identity morphisms and composition of morphisms.

We can observe that functors are some kind of "map" from a category to another, mapping both objects and morphism. The important point that it is preserving composition AND identity morphism. In the context of computer science, we will work only with endomorphism in the category of type, meaning that the functors will map objects and morphism in the category of type... into the category of type.

Functors are mapping categories to other categories (source: blog.softwaremill.com)

A first example: List + map

Actually, you should already be familiar with at least with one functor: the type constructor $List$ (equipped with the map function that we already know from the previous article on Lambda Calculus and Currying). Why is that ? Because you can view the type constructor List as mapping any type $A$ to a type $List[A]$, while the $map$ function will map any function of type $A \to B$ to a function of type $List[A] \to List[B]$.

Recall that the map function could be defined in python as:

def mapList(func: Callable[[A], B]) -> Callable[[List[A]], List[B]]:
    return lambda xs: [func(x) for x in xs]

Functors and Type Constructors

More generally, in computer science, a functor can be viewed as a type constructor $F$ equipped with the higher order function $fmap$ which from any function of type $A \to B$ returns a function of type $F[A] \to F[B]$. This concept is very powerful because this pattern alows one to apply a function inside a generic type without changing the structure of the generic type, as we usually do while using the map functions in the case of lists. Functors are already pre-defined in Haskell, but following our definition, it could be written as:

class Functor f where
    fmap :: (a -> b) -> f a -> f b

A second example: Maybe Functor

Let’s mention another example: the Maybe functor. Maybe is a type constructor which is defined as:

data Maybe' a = Nothing | Just' a

Maybe enables you to model a value that may or may not be present. It can be very useful to use this for robust programming. In languages like C# and Java, most things can be null, which can lead to much defensive coding. What happens more frequently, though, is that programmers forget to check for null, with run-time exceptions as the result. A Maybe value, on the other hand, makes it explicit that a value may or may not be present. In statically typed languages, it also forces you to deal with the case where no data is present; if you don’t, your code will not compile.

Its fmap function can be defined as:

instance Functor Maybe' where
  fmap f (Just' x) = Just' (f x)
  fmap _ Nothing  = Nothing

meaning that Maybe is also a functor.

Example with Python and Haskell

Python and Haskell are two popular language used for functional programming. Python is a general-purpose language that was designed to be easily understood and used by beginners. It supports functional programming paradigms, such as lambda expressions and higher-order functions, and allows for efficient data processing. On the other hand, Haskell is a more advanced language that was designed for professional developers who need a deep understanding of functional programming concepts. Haskell has a strong type system and uses lazy evaluation to make programs more concise and efficient. While people usually do not explicetely write Functors (or Monads) in Python, Haskell emphasizes Functional Programming and the use of categorical concepts.

Let’s consider the following problem. We want to consider a pile of papers with some values of some type on each of the side of the paper. Let’s represent this in python:

from typing import Generic, TypeVar, List

T = TypeVar("T")
T = TypeVar("U")

class Paper(Generic[T]):
    def __init__(self, cover: T, back: T):
        self.cover = cover
        self.back = back
paper1: Paper[List[float]] = Paper([1.0, 3.0, 5.0], [2.0, 3.0, 5.0])

Let’s imagine that we want to compute the sum of the values for each side of the paper1, and instanciate a Paper object with the sum of the values in each side. The naive version would be to write:

paperSum = Paper(sum(card1.cover), sum(card2.back))

It means that each time you want a function on a Paper object, you need to apply it twice, on each side. But perhaps we could try to use a functor in order to transform any function of type $A \rightarrow B$ into a function of type $Paper[A] \rightarrow Paper[B]$.

def fmap_paper(func: Callable[[T], U]) -> Callable[[Paper[T]], Paper[U]]:
    return lambda paper: Reversible(fun(paper.cover), fun(paper.back))

It means that Paper is a functor. Now, we solve the problem more easily:

    paper_sum2 = fmap_paper(sum)(paper1)

Much better right ? It means that we can convert a function and then apply it to a paper object (as long as the types are compatible). Things are simpler in Haskell, since Functors are native. We just have to define its type and fmap method.

data Paper a = Paper
    { cover :: a
    , back :: a
    } deriving (Eq, Show, Read)

instance Functor Paper where
    fmap :: (a -> b) -> Paper a -> Paper b
    fmap f (Paper x y) = Paper (f x) (f y)

paper1 = Paper [1.0, 3.0, 5.0] [2.0, 3.0, 5.0]
paperSum = fmap sum paper1

Now, in the ghci, it gives:

ghci> paperSum
Paper {cover = 9.0, back = 10.0}
ghci> paper1
Paper {cover = [1.0,3.0,5.0], back = [2.0,3.0,5.0]}

Now let’s suppose that we have a journal, defined as list of papers with text. We want to define a function paperSummary that would select the first letter of each paper and concatenate them in a new paper. Let’s write it in Haskell:

charToString :: Char -> String
charToString c = [c]

concatPapers :: Paper [a] -> Paper [a] -> Paper [a]
concatPapers (Paper xs as) (Paper ys bs) = Paper (xs ++ ys) (as ++ bs)

paperSummary :: [Paper String] -> Paper String
paperSummary xs = foldl concatPapers x0 listPapers
    where
        x0 = Paper "" ""
        listPapers = map (fmap $ charToString . head) xs

In this piece of code, we are composing charToString and head and applying it to each side (using fmap) for each paper of the list (using map). Then, we reduce the list of papers into one paper using foldl (similar to reduce in python) and concatPapers. We did not need to duplicate the code for each side, and did not need to write any loop.

Let’s apply the function to a new example:

papers = [Paper "Hello" "Pedro", Paper "Array" "YMCA", Paper "Story" "Tartar", Paper "Kiwi" "Helicopter", Paper "Elie" "Obvious", Paper "Laurel" "New", Paper "Land" " "]

papersSum = paperSummary papers

It gives:

ghci> papersSum
Paper {cover = "HASKELL", back = "PYTHON "}

Conclusion

I hope you enjoyed this introduction to Category Theory. It is one of the most abstract branches of mathematics, but I think that its most basic concept can be explained in simple terms. Like programming, categories are about structure, and we saw that it provides the language to make programs simpler and more beautiful. For more information on Category Theory, I recommend the following book. In my next post, we’ll take it a step further by discussing Monads, another fundamental concept in Category Theory.